Introduction
The world is in a period of rapid change. The most recent report from the Intergovernmental Panel on Climate Change (IPCC, 2022: 33) sets out the devastating harm caused by global heating that is threatening the possibility of a ‘liveable and sustainable future for all’. Mathematics is deeply implicated in climate change and other global issues, for example, in how events are communicated and modelled. Models of climate, pollution, virus spread and the economy have real-world effects, and mathematics is also implicated in the creation of global challenges facing humanity. The fallibility of mathematics allows it to be used for unjust purposes. Mathematical models of the economy, which place no value on materials before they are extracted, facilitate exploitation of resources and the depletion of environments which have historically sustained communities. This article addresses the issue, in such a context, of what is the role of mathematics teacher education and, in particular, what can mathematics teacher educators (MTEs) do in supporting teachers to respond to global challenges, and associated injustices, within their mathematics classrooms?
In the next section, we develop a framework from ideas of critical mathematics education (CME). We follow Andersson and Barwell (2021) in identifying three schools of CME: Freirean (Freire, 1970; Gutstein, 2006); Foucauldian (Walkerdine, 1988); and Nordic (Skovsmose, 1994). We draw out commonalities and differences, and we report on work taking place in one university where, since 2015, MTEs (including the two authors of this article) have been encouraging teachers on a one-year teacher education course to address global issues in their classrooms. The lens of CME offers a mechanism for reflection on the role of the MTE and for questioning of assumptions.
In a concluding section we reflect on how, in England, the spaces for responding to global challenges, as educators, appear squeezed in an education system increasingly influenced by conservative political forces. For MTEs, a mandated core content of initial teacher education which conceptualises teaching, and learning to teach, as apolitical, context-free and as a technical endeavour, precludes a sustained focus on global challenges. We reflect on what spaces for action exist even within such constraints.
Critical mathematics education
In recent years, there have been increasingly urgent articulations of a socio-political perspective of mathematics education (Valero, 2004; Gutiérrez, 2013). Such a perspective places mathematics education within a historical, social and political lineage, and thereby points to blind spots that may simply have become invisible to practitioners, such as how power, knowledge and subjectivity are assigned and used. We recognise important strands within this perspective, such as that of socio-critical modelling (Kaiser and Sriraman, 2006: 304), ethnomathematics (Powell and Frankenstein, 1997) and, more recently, work on Indigenous ways of knowing (Nicol et al., 2020).
CME is another strand, which refers to work which brings insights from critical theory into the sphere of mathematics education. Andersson and Barwell (2021: 3, emphases in original) offer a summary, stating that CME ‘is driven by urgent, complex questions; is inter-disciplinary; is politically active and engaged; is democratic; involves critique; and is reflexive and self-aware’. This characterisation says to us that CME is particularly appropriate to a consideration of how issues such as climate change might be relevant to the work of an MTE. Global challenges such as the climate emergency and other ecological disasters are certainly urgent, complex and interdisciplinary, and addressing such questions as an MTE is unavoidably political. We hope to demonstrate the use of CME as a tool for critique and reflexivity.
As mentioned above, Andersson and Barwell (2021) identify three broad schools of work within CME (acknowledging that such divisions are a simplification). We consider each school in turn, and the extent to which research, bringing a CME perspective, has considered issues around climate change education, as well as any work within mathematics teacher education drawing on that school.
Freirean school
The Freirean school is focused on the use of mathematics for consciousness raising, for ‘reading the world’, in a way that draws parallels to Freire’s (1970) work on literacy (Andersson and Barwell, 2021). Frankenstein (1983) offered a seminal articulation of an application of Freire’s epistemology in the context of mathematics education, applying Freirean ideas to teaching urban working-class adults. Gutstein (2016: 455, emphasis in original) proposed the idea of an education where students are taught to ‘read and write the world with mathematics’, drawing on Freire and the tradition of critical pedagogy, where reading the world with mathematics means:
These are not the kind of statements that appear on typical school curriculum documents. However, part of reading the world is also, for Freire, reading the ‘word’; in other words, developing literacy skills. In parallel, Gutstein views it as axiomatic that a mathematics education aimed at liberation must mean that students learn what he labels ‘classical’ mathematics, alongside the reading of the world. This is important in terms of access to opportunities for themselves and families. Equally crucial, what needs to accompany the work of reading is the work of writing the world with mathematics, that is, making changes in the world and developing ‘social and individual agency’ (Gutstein, 2016: 456).to use mathematics to understand relations of power, resource inequities, and disparate opportunities between different social groups and to understand explicit discrimination based on race, class, gender, language, and other differences … to dissect and deconstruct media and other forms of representation … to use mathematics to examine these various phenomena both in one’s immediate life and in the broader social world and to identify relationships and make connections between them.
Gutstein’s (2016) research took place in an urban high school in Chicago. He based his teaching on the generative themes of his students’ lives and communities, that is, the social contradictions and tensions which, through education, can become sites for developing new consciousness and critical action. Freire (1970) and Gutstein (2006) draw attention to the need for a generative and cyclical relationship between hope and struggle, that is, each one needing the other to be sustained. Crucially, a theme only becomes generative once it prompts action.
Gutstein (2006: 5, 7) suggests that a key element of critical pedagogy is that learners ‘look for underlying explanations for phenomena, and question whose interests are served and who benefits’, and engage in a ‘systematic search for the roots causes of injustice’. He concludes: ‘education should, above all, develop full, ethical, loving human beings who care about and act in the world for peace and justice. If that is so, then the question of how and why we use what we learn must be part of everything that we do in education. Everything’ (Gutstein: 2016: 493). Gutstein (2016) reflects that, at the time of writing (and we believe it still to be true today), no other research has been reported where a CME approach has been adopted over an entire academic year. In all other cases, applications of Freire’s ideas within CME have been short programmes, one-offs, or taking place in out-of-school settings. This is a sobering fact.
There are a small number of studies within mathematics education, inspired by Freire, that touch on climate change. Of note is Renert’s (2011) proposal for a ‘sustainable mathematics education’ that draws on wider ideas of education about, for and as sustainability (Sterling, 2004). Renert’s (2011) approach is one we read (with Gellert, 2011) as being consistent with a Freirean CME.
The Freirean school of CME is tied closely to concepts of social justice, and there have been several articulations of what a social justice lens might mean in considering mathematics teacher education (Stinson and Wager, 2013; Gates and Jorgensen, 2009). A double special issue of the Journal of Mathematics Teacher Education 12 (3 and 6) focused on social justice (associating ‘radical’ social justice with the ideas of Frankenstein [1983]), and included several articles on initial teacher education: de Freitas and Zolkower (2009) draw on Bourdieu in disrupting patterns of discourse; and Boylan (2009) links social justice in teacher education to questions of emotionality.
Foucauldian school
The Foucauldian school investigates the (often invisible) uses of the discourses of mathematics in the ‘organization of human affairs’ (Andersson and Barwell, 2021: 9), for instance, the way in which middle-class assumptions about what constitutes child development can become accepted as what it means to be ‘normal’, or the way in which differences between girls’ and boys’ relations to mathematics are constructed (Walkerdine, 1988).
Although Foucault’s ideas have been used extensively within mathematics education, much of this work has not been labelled explicitly as CME. However, such work generally aligns with aspects of CME, such as being politically active, involving critique and reflexivity. Foucault’s notion of discourse is of particular significance from a critical perspective. For Foucault (1972: 49), discourse goes beyond words and acts of speech, and refers to ‘practices that systematically form the objects of which they speak’. What distinguishes discourse from language is context, since discourses only make sense within contexts (Walshaw, 2007). According to Foucault, discourses ‘are not about objects; they do not identify objects, they constitute them and in the practice of doing so conceal their own invention’ (Ball, 1990: 2). Discourses do more than give meaning (or truth) to the world; they create it by producing varying subjects, going beyond what people say and do, to ‘organising actual people and their systems’ (Walshaw, 2007: 41, emphasis in original). Put another way, ‘There are no behaviours which exist outside the practices for producing them’ (Walkerdine, 1989: 271). Thus, a Foucauldian perspective speaks particularly to issues of ‘human biases, blind spots and structures of dominance and oppression’ (Andersson and Barwell, 2021: 7), with which the work of CME concerns itself. Foucault’s ideas have therefore been used as a framework to expose power structures and reveal ‘taken as natural’ aspects of practices (Hardy, 2004: 106) that permeate all levels of teaching and learning mathematics.
Mathematics education discourses will each position and categorise learners and teachers in differing ways (Hardy, 2000). By deploying Foucault’s notions, Pais and Valero (2012: 9) examine how the field of mathematics education research ‘fabricates its object of research’, that is, generates its own discourses, to address the objects ‘learning’ and ‘mathematics’. In certain deficit discourses, learners may be categorised as ‘struggling’, ‘low ability’, ‘unconfident’ or even ‘anxious’, and marginalised groups are formed. Teachers can be categorised as ‘lacking subject knowledge’ or they may be described as ‘traditional teachers’. Likewise, learners may be positioned as ‘gifted’ and teachers as ‘progressive’, and notions such as ‘good teaching’ and ‘best practice’ permeate. Foucault’s concept of normalisation is the process by which subjects are categorised into normal or abnormal (Hardy, 2004), a process that, when coupled with Foucault’s concept of power, also determines what is viewed as valid knowledge. It is through surveillance (high-stakes assessments, progress measures, league tables, school inspections, reward systems, student groupings and so on) that categorisation and normalisation are compounded.
The concept of normalisation has been applied in various ways by a range of mathematics education researchers. Walkerdine’s (1988) early work from a Foucauldian perspective, for example, demonstrated that the notion of a ‘child’ is a fiction, a product of discursive practices, practices that are produced in particular social settings through language.
We are not aware of any work relating climate change directly to a Foucauldian CME. In mathematics teacher education research, and drawing on Foucault, Llewellyn (2009) warns of the dangers of labelling prospective teachers using classifications such as gender, social class or ethnicity, labels that are potentially reinforced or even created by the research community.
Nordic school
In the Nordic school, Skovsmose (1994) explores the use of technology in society and argues for the need for students in school not only to be taught to do mathematics, but also to critique how mathematics is used and how it gets embedded in technologies which have real social effects, such as algorithms for welfare payment distributions. At its most general, Skovsmose (1994: 38) argues that for an education to be ‘critical’, it must engage with ‘social contradictions’, an idea that recalls Freire’s (1970) generative themes.
There are two sets of ideas proposed by Skovsmose which are particularly relevant to work in teacher education. One is Skovsmose’s (1994) articulation of three forms of knowing: mathematical, technological and reflective. Mathematical knowing is what Gutstein (2016) refers to as classical, which includes the mastery of algorithms and the skills needed to reproduce proofs and apply theorems. Technological knowing refers to the application of mathematics, particularly in the form of modelling. This kind of knowing is ‘necessary for using a technological tool in pursuing some technological aim’ (Skovsmose, 1994: 47). Reflective knowing ‘refers to the competence in reflecting upon and evaluating the use of mathematics … evaluations of the consequences of technological enterprises’ (Skovsmose, 1994: 47). This last form of knowing we view as synonymous with Gutstein’s (2016) use of critical knowledge. Given that our focus is on working with teachers, we extend reflective knowing to include reflecting on mathematics teaching and its purpose, to include reflections on the kind of classroom interactions and ways of being that teachers want to engender.
The second set of ideas relates to Skovsmose’s (1992) notion of the formatting power of mathematics, that is, the way in which mathematics, and particularly the technology and the models that it sustains, has real social impact. Skovsmose (1992) uses the example of the modelling by airlines of non-arrivals, which leads to over-booking of planes and the real consequences this can have. More sinister examples extend to the ordering and accessibility of vaccines, predictive policing and the use of algorithms in job hiring (O’Neill, 2016). One of the aims of reflective knowing can be to bring attention to this formatting power of mathematics and the human, contingent decisions that lie behind all models and technologies, and the injustices they may produce.
It is within this school that we have found most connections (compared to the other two schools) to past work on the specific issue of climate change. Of particular note in this regard is the work of Barwell (2013) and colleagues (Hauge and Barwell, 2017; Barwell and Hiis Hauge, 2021), who also draw on post-normal science in their work. Also of note is work taking place in Norway (for example, Steffensen et al., 2021).
Uses of the Nordic school within mathematics teacher education are limited. Gerdes (1998) draws on the critical tradition in mathematics education to argue for the need for MTEs to attend to the culture of prospective teachers, and to use that culture in supporting their development as teachers. We found few other studies. In marking this relative absence, we acknowledge that substantially more work has linked teacher education with ethnomathematics, but, mainly for reasons of space, we are not reviewing that work. We view one contribution of this article as proposing the possibilities of bringing CME into use in the context of mathematics teacher education.
A framework for considering mathematics teacher education from a critical perspective
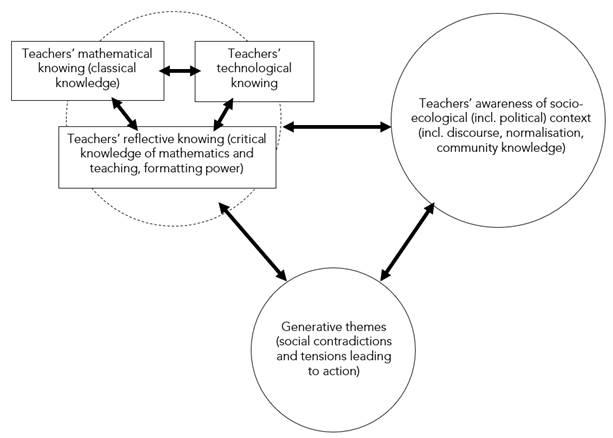
We do not adopt one particular school of thought within CME, but rather use the range of meanings to investigate the role of an MTE. We use the broad characterisation of the three schools of CME as a set of ideas, offering opportunities for reflection and critique of the practices of MTEs. Gutstein (2016) offers a diagram for how community knowledge can be connected, via the identification of ‘generative themes’, to what he labels as classical and critical knowledge. We have been inspired by this diagram to offer a version (see Figure 1), focused on the work of teachers of mathematics, which helps us think about our work as MTEs. We have drawn on each school: taking from the Freirean school the concept of generative themes; taking from Foucault the significance of the sociopolitical, to which we add the significance of the socio-ecological (Coles, 2022); and taking from the Nordic school the three forms of knowing and the formatting power of mathematics. To exemplify the framework, a teacher may recognise the significance of air pollution in their local area and decide they want to research it; at the point they then decide to offer something in their classroom on this topic, their awareness of the socio-ecological issue of air pollution has become a generative theme for them, since it has linked to actions. Through the process, the teacher is likely to have developed some technological knowing, to come to some model of the situation. Through offering a task to their students, it is likely that some reflective knowing, about the kind of teacher they want to be, may emerge.
We use Figure 1 to reflect on where we prompt attention and awareness (as MTEs), and where we might prompt but do not. In the next section, we report on a long-term project that is ongoing at the University of Bristol. This is a project that embodies a process of curriculum innovation within our teacher education course (across subjects), and it is not guided explicitly by ideas of CME. We offer a description of this project, before reporting on outcomes via a reflection on three professional journal articles. We move on to consider wider systemic issues around such work, and what else might be possible within politically constrained contexts.
The Green Apple project
The name ‘Green Apple’ came from the internal funding scheme which helped kick-start the project in 2015. The funding was to support innovation in our one-year teacher education course for secondary school, which leads to a Postgraduate Certificate of Education (PGCE). The idea was to support teachers bringing questions of global challenges into their subject teaching, or their work as form tutors (a pastoral role required of teachers in England). Two (or more) ‘Green Apple representatives’ (reps) are recruited from each of the eight subjects offered on our PGCE course, and these reps meet with a group of teacher educators (including MTEs) on three or four occasions during the year. The reps are responsible for disseminating outcomes from meetings to the rest of their subject group. Meetings introduce reps to ideas (such as different framings of ‘education for sustainable development’), allow time for discussion between and across subject groups, and lead to prompts for action. Classroom resources are shared, and previous years’ work is available. The project has taken an increasingly prominent role on the whole course, with all prospective teachers expected to engage in some actions in their schools.
Methodological approach to analysis
To present some of the outcomes of the project, and to focus on the role of the MTE, we report on three articles written by mathematics teachers linked to the Green Apple project which have appeared in a professional journal. These are the only professional publications from the Green Apple group, and the writing forms the data for our analysis. Our rationale for focusing on published materials is that these are the only resources we have that contain reflections on the process of their development, something which was necessary for our analysis. In what we report here, we focus on the tasks offered and the role of the MTE, drawing on our framework (Figure 1).
Figure 1 is essentially about the noticing and actions of teachers. Consistent with this focus, and following ideas from the discipline of noticing (Mason, 2002), we first offer an account of the three pieces of writing, avoiding evaluative comments and aiming to provide readers with enough detail to make sense of our analysis, without having to read the articles themselves. We then move into an account for the writing, at which point we used Figure 1 to frame our reflections. We asked ourselves whether the MTEs involved had a role in provoking awareness, or identifying generative themes, or in supporting a focus on particular forms of knowing. As authors, we had more or less prominent roles in each case (Alf more in the first and third, Tracy more in the second). The one with the smaller role led the analysis of that section, to try to disentangle what contextual knowledge we bring to the analysis, compared to the data actually present in the professional articles. We have written as ‘we’, as we went through a process of presenting our analyses to each other and discussing alternatives.
Sustainable futures, 2018
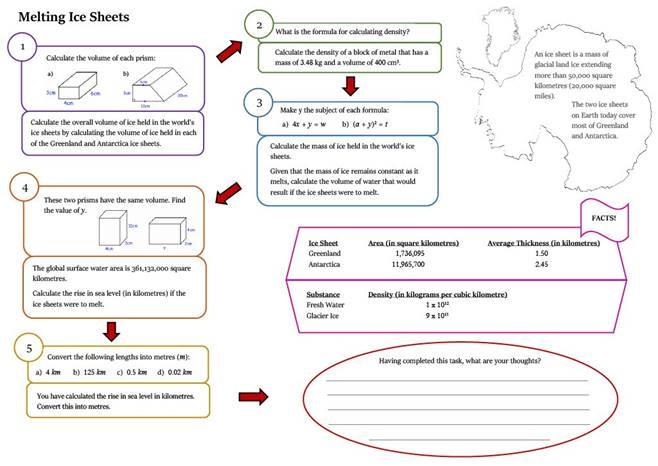
Karl Bushnell (2018) wrote an article based on resources he had developed and trialled for his own classroom. Karl received his PGCE from the University of Bristol and played an active role in the Green Apple project. The work he wrote about was conducted when he had taken up a job in a school near Bristol. Karl continued his Master’s in Education at the University of Bristol, and developed an approach to offering tasks which paralleled standard exercise questions, with questions that led students to answers which told them something about the global environment. An example is given in Figure 2, which shows the worksheet for students, involving a sequence of tasks leading them to calculate the sea-level rise that would be caused by the Greenland ice sheet melting.
In Figure 2, tasks are paired to have one question, or set of questions, with no context, and one question drawing on the same skills but in the context of melting ice sheets. For example, the second task (top right of the sheet) has three prisms and asks students to find their volume. Then the prompt is: ‘Given that the global water [sic] surface area is 361,132,000 square kilometres and using your answer to Question (1) [which was to convert 50 metres into kilometres], calculate the volume of water needed to cause a 50 m rise in sea levels.’ The final question invites students to write down their thoughts having done the calculations, that is, to reflect on the implications of the predicted change.
What can we report about the role of the MTE? The tasks were developed entirely by Karl, that is, without direct MTE involvement. We do not claim any MTE involvement in Karl’s awareness of climate change and the dangers of melting ice sheets. The danger of sea-level rise became, for Karl, a ‘generative theme’, that is, a theme that seemed relevant to him to offer to his students. Karl reflects in his writing on an experienced tension: he started with an open question about what global challenges mathematics could help with, and was then concerned that he was not able to follow up on the ideas from students, having planned the melting ice sheet task. Melting ice is a generative theme, then, for Karl, but potentially not for his students.
In the move from an awareness of sea-level rise to Karl’s offer of this theme to the class, there is some evidence of a role for the MTE. It is precisely this move (from an issue of concern, to a prompt for their classroom) that is the focus of the Green Apple project, and the subsequent support of a flexible master’s degree programme that allows teachers to follow their own classroom interests. Karl was an engaged and passionate individual who took the initiative to continue to develop themes from the Green Apple project after he had left the PGCE course as a qualified teacher.
In terms of the type of knowing that is being aimed at through this task, there is attention to mathematical knowing and some evidence of technological knowing, in the sense of the process of the worksheet as offering a modelling solution to the question. Karl himself has used or developed technological knowing in deriving the model. There does not appear to be attention to reflective knowing about mathematics or the formatting power of mathematics, although there is an open prompt to students at the end: ‘What are your thoughts?’ In other words, the mathematics is presented as a neutral tool, and the assumptions behind the model being used are not discussed. The MTE did not provoke questions about this neutrality, nor, for example, prompt reflection on possible links to social action or oppressions which are entailed in the causes of sea-level rise (for example, consideration of the almost incalculable human suffering which would ensue). Karl shows reflective knowing in his writing about his teaching, when he comments on wanting to do more to link his teaching to real issues.
Global challenges, 2019/20
Across two articles (Brown et al., 2021a, 2021b), nine prospective teachers on the PGCE course (in the 2019/20 cohort), supported by their three MTEs, each wrote about one task they had either created or found and then used (or planned to use) with classes for which they were responsible, in their placement schools. By this time, several years into the Green Apple project, global challenges were written in to one of the PGCE programme’s master’s assignments, and so every prospective teacher had to engage, in at least one lesson, with thinking about how to incorporate an issue such as climate change into their classroom teaching. As MTEs, having seen and been impressed by the work developed by these teachers, we proposed some joint writing. We helped edit and structure the writing, and supported its submission. Below, we report five of the nine tasks described across the articles. Two tasks began with simply stated challenges to provoke discussion, which then developed into more extended activity: ‘How does a country’s GDP [gross domestic product] affect a person’s life?’ (Brown et al., 2021a: 9); ‘How many trees could fit in this room?’ (Brown et al., 2021b: 9).
The other tasks got students doing some work or calculations that did not initially relate to a global challenge, and then led into a key question, for example: ‘Based on data about incomes in England and Romania: “Which country has a bigger pay gap between male and female workers?”’ (Brown et al., 2021a: 10); ‘Based on drawing paths and associated loci (to model a potential Covid transmission distance of 2m): “assess potential transmission points.”’ (Brown et al., 2021a: 13); and ‘Having worked out the area of the school grounds and based on aerial photographs of deforestation in Brazil: “find the area that had been cut down, and how many ‘areas of the school’ that this represented.”’ (Brown et al., 2021b: 11).
There is one obvious shift here in the role of the MTE, in that there is a mandating of some exploration of global issues, which could be viewed as a provocation to find at least one theme generative for each teacher. As with the previous example, these tasks, and the MTE support for them, appear primarily focused on mathematical and technological knowing. The write-ups of the tasks suggest that wider implications about society and links to social activism were left implicit, and that would also be true to say about the MTE support being offered (that is, consideration of such wider issues was neither prompted nor provoked). In other words, reflective knowing about mathematics is again absent from the task design and, we can therefore assume, from the prompting of the MTEs. As with the first case, there is some evidence of the work prompting reflective knowing about teaching and the kinds of classroom that teachers want to develop.
Climate science, 2021
In early 2021, Alf began a collaboration with a scientist (Joseph Darron) from the UK Met Office, after this scientist was given a secondment to work at the University of Bristol. Joseph’s research centres on questions of how climate models and statistics are communicated (for example, to politicians). After some discussions about making Joseph’s research into something usable in the classroom, Alf invited a local partner school to see if they were interested in collaborating. One teacher (Barney Rolph) volunteered, and he worked on adapting and trialling the tasks that we had been developing. Barney had been on the PGCE course at the University of Bristol, and he had been involved in the Green Apple group. The task Barney used in his classroom was the following (Coles et al. 2022: 5):
In the article, Barney offers some of the responses of his class, and the further work he went on to do with them using climate data.Climate models are used to simulate the climate and predict changes. We will be focusing on models that can be used to predict how much wetter or drier a place might be in the future. There are different models, made by different scientists.
Botswana (in Africa) currently averages around 34mm of rain per month.
Here are 9 projections for the change in rainfall in Botswana (in mm per month) in the coming years:
+17; +13; +6; −2; −2; −6; −6; −6; −14
Your task:
Imagine you are an advisor to farmers in Botswana. You are going to prepare a written summary of this data advising farmers of future risks and changes to the climate. Think about different mathematical techniques that you have learnt that might help analyse and/or present this data.
The MTE role is quite different in this case, compared to the previous two. Here, the MTE acts as a conduit between a climate scientist and a teacher. As the MTE involved, Alf remembers recognising, in Joseph’s presentation of his research, its classroom potential. There is perhaps evidence here of Alf recognising a generative theme for himself, and one that could be generative for other teachers. The questions with which Joseph was grappling, to do with the consequences that different presentations of data have for how those data are interpreted, seemed like ones that students in schools could access. Alf also recognised that the data Joseph was using seemed accessible for quite young students and, in our experience, it is not easy to find real data in a form that is suitable for a classroom.
The task, in contrast to the previous ones, feels as if it does begin to touch on questions of reflective knowing about mathematics. There is reflection on the use of mathematics and how complex data might be summarised mathematically. Hence, we also interpret the MTE role in this case as provoking awareness of reflective knowing in mathematics, alongside technological and mathematical knowing. Barney reflects, at the end of the article, on wanting to find more tasks without single answers to use in his teaching.
Conclusion
Having presented the work of the Green Apple project, as it has manifested in three professional journal articles, and having offered an analysis of the role of the MTE in each case, we now summarise and reflect further on our findings. Our aim has been to address one key question: What can MTEs do in supporting teachers to respond to global challenges, and the associated injustices, within their mathematics classrooms?
As alluded to above, we interpret the MTE roles in the first two cases as being linked to the raising of generative themes and the development of mathematical and technological knowing and reflective knowing about teaching, and, only in the third case, with a shift into reflective knowing about mathematics. Considering the second example, there seems to be a power in mandating engagement in considering global challenges, as part of a teacher education programme, and supporting further engagement of those who show interest, by setting up and coordinating a co-writing opportunity. In the final example, the use of mathematics by politicians, policymakers and scientists is beginning to be explored in the task, in contrast to the previous two articles. In this third example, the MTE appears to act as a hub or catalyst.
In all cases, our framework of CME points to possibilities for the MTE that were not taken. In Karl Bushnell’s work, a possible MTE provocation might have been to invite consideration of the accuracy of the model, or the way in which sea-level models are being used to guide policy around the world, and whether such models impact on particular groups – is it marginalised groups who are forced to live in high-risk areas? In the case of the 2019/20 writing, similar provocations might have been: How is GDP calculated? What is left out of GDP, and what is the impact? How can we model the carbon stored by trees? In the climate model scenario (the third example), again, we did not address questions of the impacts of drought or flood on different sectors of society. Other prompts might have been linked to the development of the generative themes in the first place, and a suggestion of trying to engage students in what socio-ecological issues concern them and their families.
In England, it is unlikely that the wider questions would be addressed in a mathematics classroom, but, in reflecting on MTE roles not taken, these seem like potentially significant provocations for teachers, in forcing a consideration of how global issues link to the organisation of societies and the inequalities which are exposed by global forces, such as climate change.
As demonstrated here, the framework of CME (Figure 1) offers a mechanism for recognising what is not being done, as an MTE. Questions we might ask ourselves (for example, in planning to work with prospective teachers) are:
Despite the developments evident over the seven-year period of the Green Apple project, we are left with a sense that the resources developed by teachers, and the related work of MTEs, remain on the margins. The tasks developed seem to represent likely one-offs in the teachers’ practices. Similarly, for the MTEs, a one-year teacher education course, which includes 12 weeks or less at university with prospective teachers, along with the need to show coverage of a mandated ‘core content’ of initial teacher education, make any sustained focus on global challenges next to impossible; hence, support for such work also has a ‘one-off’ feel.What are the global challenges that teachers we are working with care about? What about the communities they work with? What tasks and mechanisms (for example, as part of a teacher education course) can we offer, to support them acting on their, and their students’, interests in their own classrooms? (Developing generative themes)
When does mathematics teaching reinforce, or remain silent about, inequalities embedded in the wider organisation of society, including mathematical models? Do we call attention to such absences? What might teachers’ lived experiences of inequality be, and what sensitivities will be needed to explore this (for example, the space and safety to express reactions and know they have been heard)? (Reflective knowing)
In any context of mathematics teaching (including our own), do we invite reflection on the uses of the mathematics being learnt? Can we link with a professional who is working on a global challenge, and explore the reality of their use of mathematics? How might we make resources available for teachers in a form that provokes reflection on the uses of mathematics? (Awareness of socio-ecological context; mathematical, technological and reflective knowing)
For both teachers and MTEs, there are demands that are hard to ignore (examination success in school; passing a teaching qualification in teacher education courses), both of which, in England, pull away from a focus on global challenges. So, although we have provided some answers to our question about the possible roles of an MTE in supporting such work, we are struck by the limited nature of the roles we have been able to embody, in comparison to the complexity and depth of the issues facing the planet, and amid conservative pressures on educational decisions in England that, to take one example, mandate against the use of particular resources in schools. (Government guidance to teachers in England from 2020 banned the use of materials produced by any organisation taking an ‘extreme political stance’, which includes any organisation judged to be promoting ‘anti-capitalism’.)
One thought that sustains us, however, is that we are developing MTE practices, roles and resources to support a curriculum-in-waiting. Covid-19 has shown how rapidly changes can be made in education systems. Over the seven years of the Green Apple project, we have sensed prospective teachers increasingly wanting to work on interdisciplinary and global issues, through the lens of their subject teaching. We suggest that CME offers a ready, and largely untapped, set of resources to help MTEs think about possibilities for transformation in their roles and practices, and we hope that the framework we have developed (Figure 1) might support such use. One hope we have is that prospective and in-service teachers will increasingly demand such change. Although our framework, and the prompts above, are framed around mathematics, we imagine other subject labels could be substituted, to provoke reflection more broadly about teaching and teacher education.
Without wanting to sound utopian, we also see possible roles for an MTE, even within contexts of tight constraint and a mandated curriculum for teaching and teacher education. Although generative themes for teachers may not have the scope to touch on socio-ecological issues, we believe that considering generative themes within the mathematics curriculum, coming out of an awareness of the wider context of a school, is potentially important work. We have been asking ourselves, what could MTEs do that might support teachers, in at least developing the skills to address global challenges and associated inequalities in their classrooms, even if such content is impossible to address directly? We imagine possible themes, within a constrained curriculum, to include the importance of mathematical proof, or student explanations of their reasoning, and collaboration on mathematics.
We also see a role for the MTE in questioning the forms of knowing that are the aim of any teaching. As MTEs we might be attuned to noticing and questioning assumptions from prospective teachers. The framework in Figure 1 might help an MTE notice what a teacher is, and is not, doing. As MTEs, we might be attuned to assumptions such as:
-
-
There are answers to all problems.
-
-
There is a correct way of doing something.
-
-
There is a best way of solving a problem.
-
-
There are processes we can follow that, when applied properly, will lead us to the answer.
-
-
We can get to a neat solution, given any problem.
-
-
Real life can be simplified to a model.
-
-
What would my classroom look like if there are always different answers considered?
-
-
What would my classroom look like if there is always a recognition of uncertainty?
-
-
What would my classroom look like if speakers always make assumptions explicit?
Declarations and conflicts of interest
Research ethics statement
Not applicable to this article.
Consent for publication statement
Not applicable to this article.
Conflicts of interest statement
The authors declare no conflicts of interest with this work. All efforts to sufficiently anonymise the authors during peer review of this article have been made. The authors declare no further conflicts with this article.
References
Andersson, A; Barwell, R. (2021). ‘Applying critical mathematics education: An introduction’. Applying Critical Mathematics Education. Andersson, A, Barwell, R R (eds.), Leiden: Brill, pp. 1–23.
Ball, S. (1990). ‘Introducing Monsieur Foucault’. Foucault and Education: Disciplines and knowledge. Ball, S (ed.), London: Routledge, pp. 1–8.
Barwell, R. (2013). ‘The mathematical formatting of climate change: Critical mathematics education and post-normal science’. Research in Mathematics Education 15 (1) : 1–16, DOI: http://dx.doi.org/10.1080/14794802.2012.756633
Barwell, R; Hiis Hauge, K. (2021). ‘A critical mathematics education for climate change: A post-normal approach’. Applying Critical Mathematics Education. Andersson, A, Barwell, R R (eds.), Leiden: Brill, pp. 166–84.
Boylan, M. (2009). ‘Engaging with issues of emotionality in mathematics teacher education for social justice’. Journal of Mathematics Teacher Education 12 (6) : 427–43, DOI: http://dx.doi.org/10.1007/s10857-009-9117-0
Brown, J; Coles, A; Hayward, R; Helliwell, T; Lustig-Bruce, D; Owen, E; Salt, A. (2021a). ‘Mathematics teaching and global challenges: Part 1’. Mathematics Teaching 276 : 9–12. https://www.atm.org.uk/mathematics-teaching-journal-archive/176131 . Accessed 2 December 2022
Brown, J; Coles, A; Helliwell, T; James, I; Kurian, H; Läderach, J; Morris, L; Sebe, I. (2021b). ‘Mathematics teaching and global challenges: Part 2’. Mathematics Teaching 277 : 11–13. https://research-information.bris.ac.uk/ws/portalfiles/portal/298732706/MT_part_2.pdf . Accessed 2 December 2022
Bushnell, K. (2018). ‘Learning mathematics for an environmentally sustainable future’. Mathematics Teaching 263 : 35–39. https://www.atm.org.uk/write/MediaUploads/Journals/MT263/1/MT26311.pdf . Accessed 2 December 2022
Coles, A. (2022). ‘A socio-ecological turn in mathematics education: Reflecting on curriculum innovation’. Paradigma 43 (1) : 207–28, DOI: http://dx.doi.org/10.37618/PARADIGMA.1011-2251.2022.p207-228.id1168
Coles, A; Darron, J; Rolph, B. (2022). ‘Communicating climate change information’. Mathematics Teaching 280 : 2–7. https://www.atm.org.uk/write/MediaUploads/Journals/MT280/02.pdf .
de Freitas, E; Zolkower, B. (2009). ‘Using social semiotics to prepare mathematics teachers to teach for social justice’. Journal of Mathematics Teacher Education 12 : 187–203, DOI: http://dx.doi.org/10.1007/s10857-009-9108-1
Foucault, M. (1972). The Archaeology of Knowledge; and The Discourse on Language. Sheridan, A (trans.), New York: Pantheon.
Frankenstein, M. (1983). ‘Critical mathematics education: An application of Paolo Freire’s epistemology’. The Journal of Education 165 (4) : 315–39, http://www.jstor.org/stable/42772808 . DOI: http://dx.doi.org/10.1177/002205748316500403
Freire, P. (1970). Pedagogy of the Oppressed. Freiburg im Breisgau: Herder and Herder.
Gates, P; Jorgensen (Zevenbergen), R. (2009). ‘Foregrounding social justice in mathematics teacher education’. Journal of Mathematics Teacher Education 12 : 161–70, DOI: http://dx.doi.org/10.1007/s10857-009-9105-4
Gellert, U. (2011). ‘Now it concerns us! A reaction to sustainable mathematics education’. For the Learning Mathematics 31 (2) : 19–20, DOI: http://dx.doi.org/10.2307/41319561
Gerdes, P. (1998). ‘On culture and mathematics teacher education’. Journal of Mathematics Teacher Education 1 (1) : 33–53, DOI: http://dx.doi.org/10.1023/A:1009955031429
Gutiérrez, R. (2013). ‘The sociopolitical turn in mathematics education’. Journal for Research in Mathematics Education 44 (1) : 37–68, DOI: http://dx.doi.org/10.5951/jresematheduc.44.1.0037
Gutstein, E. (2003). ‘Teaching and learning mathematics for social justice in an urban, Latino school’. Journal for Research in Mathematics Education 34 (1) : 37–73, DOI: http://dx.doi.org/10.2307/30034699
Gutstein, E. (2006). Reading and Writing the World with Mathematics: Towards a pedagogy for social justice. Milton Park: Taylor & Francis.
Gutstein, E. (2016). ‘“Our issues, our people – math as our weapon”: Critical mathematics in a Chicago neighborhood high school’. Journal for Research in Mathematics Education 47 (5) : 454–504, DOI: http://dx.doi.org/10.5951/jresematheduc.47.5.0454
Hardy, T. (2000). ‘Tracing Foucault’s “power” in the mathematics classroom’. Research in Mathematics Education 2 (1) : 207–24, DOI: http://dx.doi.org/10.1080/14794800008520077
Hardy, T. (2004). ‘“There’s no hiding place”: Foucault’s notion of normalization at work in a mathematics lesson’. Mathematics Education Within the Postmodern. Walshaw, M (ed.), Greenwich, CT: Information Age, pp. 103–9.
Hauge, K; Barwell, R. (2017). ‘Post-normal science and mathematics education in uncertain times: Educating future citizens for extended peer communities’. Futures 91 (1) : 25–34, DOI: http://dx.doi.org/10.1016/j.futures.2016.11.013
IPCC (Intergovernmental Panel on Climate Change). (2022). Climate Change 2022: Impacts, adaptation, and vulnerability, Contribution of Working Group II to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change. https://www.ipcc.ch/report/ar6/wg2/ . Accessed 6 December 2022
Kaiser, G; Sriraman, B. (2006). ‘A global survey of international perspectives on modelling in mathematics education’. Zentralblatt für Didaktik der Mathematik 38 (3) : 302–10, DOI: http://dx.doi.org/10.1007/BF02652813
Llewellyn, A. (2009). ‘”Gender games”: A post-structural exploration of the prospective teacher, mathematics and identity’. Journal of Mathematics Teacher Education 12 (6) : 411–26, DOI: http://dx.doi.org/10.1007/s10857-009-9109-0
Mason, J. (2002). Researching Your Own Practice: The discipline of noticing. London: Routledge Falmer.
Nicol, C, Archibald, J; J and Xiiem, Q.Q; Q.Q, Glanfield, F; F, Dawson, A.J.S A.J.S (eds.), . (2020). Living Culturally Responsive Mathematics Education With/in Indigenous Communities. Leiden: Brill.
O’Neill, C. (2016). Weapons of Math Destruction: How big data increases inequality and threatens democracy. London: Penguin.
Pais, A; Valero, P. (2012). ‘Researching research: Mathematics education in the political’. Educational Studies in Mathematics 80 (1) : 9–24, DOI: http://dx.doi.org/10.1007/s10649-012-9399-5
Powell, A.B, Frankenstein, M M (eds.), . (1997). Ethnomathematics: Challenging Eurocentrism in mathematics education. Albany: SUNY Press.
Renert, M. (2011). ‘Mathematics for life: Sustainable mathematics education’. For the Learning of Mathematics 31 (1) : 20–26. https://flm-journal.org/Articles/4D5553CAE27EA8E62974595DA186C0.pdf . Accessed 2 December 2022
Skovsmose, O. (1992). ‘Democratic competence and reflective knowing in mathematics’. For the Learning of Mathematics 12 (2) : 2–11. https://flm-journal.org/Articles/2DF973EBCA72E55E54AFE0A90669A.pdf . Accessed 2 December 2022
Skovsmose, O. (1994). Towards a Philosophy of Critical Mathematics Education. Alphen aan den Rijn: Kluwer.
Steffensen, L; Herheim, R; Eskeland Rangnes, T. (2021). ‘The mathematical formatting of how climate change is perceived: Teachers’ reflection and practice’. Applying Critical Mathematics Education. Andersson, A, Barwell, R R (eds.), London: Brill, pp. 185–209.
Sterling, S. (2004). Sustainable Education: Re-visioning learning and change. Tokyo: Green Books.
Stinson, D.W; Wager, A.A. (2013). ‘Teaching mathematics for social justice: Conversations with educators – A symposium (Presenters: Drs T. Bartell, B. Evan, E. Gutstein, J. Leonard; Discussants: Drs V. Hand and J. Spencer)’. Proceedings of the 7th International Mathematics Education and Society Conference (MES7, Vol. 1) . Berger, M, Brodie, K; K and Frith, V; V, le Roux, K K (eds.), Cape Town: MES7, pp. 125–8.
Valero, P. (2004). ‘Socio-political perspectives on mathematics education’. Researching the Socio-Political Dimensions of Mathematics Education. Valero, P, Zevenbergen, R R (eds.), Alphen aan den Rijn: Kluwer, pp. 5–23.
Walkerdine, V. (1988). The Mastery of Reason: Cognitive development and the production of rationality. London: Routledge.
Walkerdine, V. (1989). ‘Femininity as performance’. Oxford Review of Education 15 (3) : 267–79, DOI: http://dx.doi.org/10.1080/0305498890150307
Walshaw, M. (2007). Working with Foucault in Education. Rotterdam: Sense.